階層決定性ウォレットのセキュリティ
大抵のビットコインウォレットが準拠する規格に、階層決定性ウォレットに関するBIP32規格があり、こちらのセキュリティを深堀りした論文(ePrint)が9月末に公開されました。
Das et al. ”The Exact Security of BIP Wallets”, 2021 https://eprint.iacr.org/2021/1287
今回はこの論文の内容をご紹介しようと思います。セキュリティレベルが、BIP32規格が策定された当初想定されていたものよりずいぶんと低いことがわかった、という内容で個人的には衝撃的でした。今すぐに攻撃が成功するわけではありませんが、攻撃者が超えるべき壁が思っていたより低く、ちょっとジャンプすれば壁の上面が覗けるくらいにはなっている感じです。
階層決定性ウォレット
大抵のビットコインウォレットは入金の都度アドレスを新規発行する仕組みになっています。これって自身の銀行口座番号を都度変えているようなもので、本研究所の古株な方にとっては当たり前なことかも知れませんが、ビットコインを最近になって初めて触ったという方にとっては衝撃的な仕組みに感じることかと思います。
さて、なぜこうなっているかというと、パブリックチェーンならではの特徴がベースにあります。ビットコインを送金する場合、当たり前ですが送金相手には自身のアドレスが分かってしまいます。既存金融の常識からずれるのはここからで、ビットコインの場合ブロックチェーンエクスプローラを使えば、そのアドレスの残高を簡単に調べることができます。もし、同じアドレスを使い続けると自身の総資産がばれてしまうわけで、プライバシー上よろしくないよね、ということですね。
このプライバシー問題に対する一つのソリューションとして、アドレスを都度新規発行してしまう方法があります。でも都度新規発行するということは、自分の資産は複数のアドレスに分散することになるわけで、それらのアドレスをまとめて管理する煩雑さが伴います。
そこで、もうちょっとシンプルに運用できないか、と考案されたのが階層決定性ウォレットという技術で、この技術によりシードとよばれる元になる秘密情報から複数のアドレスを決まったルールに従って一意的に作る事が出来るようになりました。
また、図のようにツリー上に分岐を繰り返せる(端っこの葉にあたる部分がアドレスに該当します)ことから階層をもたせてアドレスを生成し管理することもできます。例えば、最初の分岐で大雑把に利用目的を分け、次の階層で受け取り用、おつり用といった使い分けを行い、その次の階層でどさーと受け取りごとにアドレスを葉として生成する、といったかんじです。
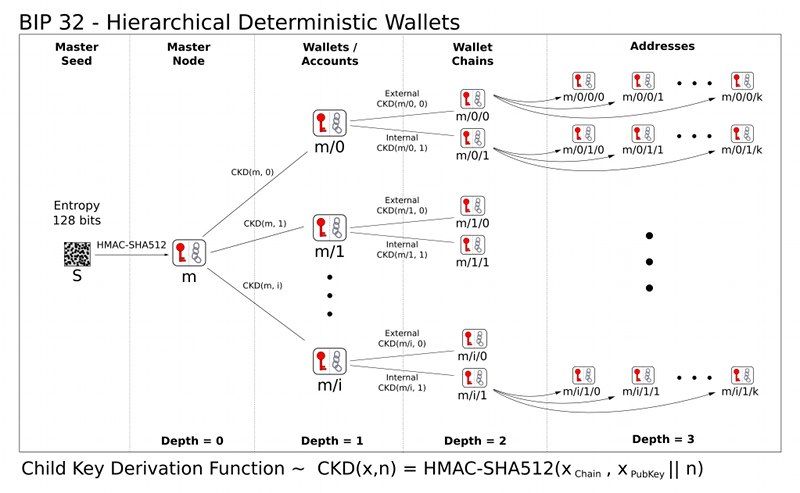
ウォレットは元にする秘密情報(シード)を保有しておくだけで、そこから派生するアドレスの束をまるっと管理することができます。まるでキーチェーンですね。
私たちのよく知っているニモニックはこの元にする秘密情報(シード)に該当し、最近のウォレットはみなニモニックを元に階層決定的にアドレスを生成し利用するスキームが搭載されています。そして、ウォレット間で互換性を持たせるのにあたり標準規格としてBIP32が提案され、今ではこの規格に準拠する実装がデファクトとなっています。
この規格のスマートなところは、シードごとに派生するアドレスは決まっていますが、別のシードから派生したアドレスとバッティングすることは実用上あり得ないことを数学的に保証している点です。そのため中央サーバーで管理する必要がなく、個々人のスマートフォンやハードウェアウォレット内でウォレットを独立して管理することができます。ビットコインらしい分散処理を引き続き実現します。
さて、こんな便利そうな仕組みだとセキュリティを筆頭に何かを犠牲にしているんじゃないか、といった心配もでてきますね。実際、階層決定性ウォレットならではの気をつけるべきポイントがあったりします。ここをおろそかにすると、秘密鍵が復元できてしまうといった大変怖い話につながったりします。
拡張公開鍵をむやみやたらに共有するな、といった運用レベルで気をつける話なのですが、今回の論文で指摘されているものからは内容が外れるため、こちらについてはまた改めて取り上げようと思います。
セキュリティレベルについて
さて、冒頭に上げた論文によると、しっかり精査したところBIP32は91ビットのセキュリティレベルを持つことが分かったそうです。
これはどういうことかというと、パラメータ値をちょっとずつ変えて秘密鍵の復号を試行する作業を2の91乗回行うと秘密鍵が復元できる(=攻撃が成功する)、といったレベルの安全性を持つよということです。では、2の91乗ってどの程度の大きさなのでしょうか。
例えば2の10乗であれば、2 x 2 x … x 2と2を10回かけて1024となります。1024通りであれば、1秒に1回試行したとして、1024秒で攻撃が成功するかんじで、余裕をもって攻撃が成功できてしまいます。
乗数の面白いところは数字が1つ大きくなるごとに、途端に試行すべき回数が増える点です。いわゆる指数関数的な増え方、と呼ばれるものになります。
2の10乗: 1024通り
2の11乗: 2048通り
2の12乗: 4096通り
…
これを91乗まで繰り返すと、凄いことになります。
2の91乗: 24758801…. と27桁の数
これは、さすがに現代のスーパーコンピュータでも試行しきれないくらいの膨大な数ではあります。
そのため、攻撃者がいくら高性能なコンピュータを用意したとしても破られることはまだなさそうです。
量子コンピュータを用いた攻撃法も研究されており、こちらについては本研究所においても田中さんが深堀りしていますので合わせてご参照ください。

さて、気になるところとしてはこの論文による精査が行われる前まではもっとずっと大きなセキュリティレベルを持つだろうと思われていた点です(少なくとも私はそう認識していました)。
ビットコインはベースの暗号技術として楕円曲線暗号を用いています。楕円曲線暗号は1985年に登場してから30年以上に渡って安全性が検証され、実利用もされててきた枯れた技術です。
一昔前までは暗号技術は最先端の軍事技術であり、国をまたいで持ち出すことすら制限される世界でした(今も一部そうした制限はあります)。インターネットの普及した現在では、主な国において方針が転換されアメリカ国立標準技術研究所(NIST)という機関が暗号の強度を調査し、利用すべきパラメータなどを整理し勧告したものを利用するといった流れが世界のスタンダードになっています。
このNISTが1999年にFIPS 186-4というドキュメントにて推奨したp-256(256ビットの大きさの楕円曲線暗号)は現在最もよく使われている楕円曲線暗号の1つで、128ビットのセキュリティレベルを持つとされています。
256ビットの意味は、秘密鍵の取り得る候補が2の256乗通りあるよ、ということです(本当は256ビットの法を持つ、なのですがここでは簡易な説明のため、こう説明します)。何も考えずに総当たりで探索をすれば、256ビットセキュリティを持つといえます。ですが、暗号方式の癖をしっかり精査することで、総当たりを試行する候補を減らす研究が進んでいます。その結果、現在知られている攻撃法を踏まえると128ビット程度のセキュリティレベルを持つだろう、とされているんですね。
さて、ビットコインですが、NISTの提案するp-256は実は利用しておらず、別のパラメータsecp256k1を用いています。また、ハッシュアルゴリズムでもマイナーなものを採用しています。
設計思想として、デファクトと違ったものを用いる事で攻撃されにくくする、といった思惑があったようです。ですが、逆に言えばマイナーなものであるがゆえに攻撃法の研究があまりされないことになります。変な穴があったとしても見落とされる可能性が大きくなります。
そんなビットコインの独特な技術選定の背景もあり、BIP32規格のセキュリティについてはあまり深堀り議論はされてきませんでした。
そのため、p-256と同様に128ビット程度のセキュリティレベルはあるんだろうな、なんて思っていたところ実は91ビットだったよ、という話だったわけなんですね。
128 - 91 = 37
と37ビットも小さかったと。
2の37乗 = 137438953472
なので、当初想定より137438953472分の1まで試行候補が絞られたことになります。
最後に、世界最速のスーパーコンピュータ富岳で攻撃を仕掛けたらどの程度で破れるかを皮算用してみます。
利用申請するつもりでRISTのサイトを覗いてみますと、富岳の整数計算能力は4.3エクサオップスだと書かれていました。
https://www.hpci-office.jp/pages/r-ccs_riken_2021a-2
1秒に4,300,000,000,000,000,000回整数の四則演算が行えるということですね。
では、91ビットセキュリティの空間をこの速度で探索できると強引に話を進めてみましょう。
計算してみると、
2^91 / 4.3e+18 = 575786064秒
で完了です!
あれ、、、
575786064秒 = 6664日 = 18.25年
おろろ、思ってたより現実的な数字がでてきましたね。
スーパーコンピュータの性能は大雑把に5年で10倍になっているようです。
5年後には2年弱の試行時間で、そのまた5年後には、66日間の試行時間で済むことになります。
ただちに問題になるわけではなさそうですが、ちょっと現実味ある数字ではあります。
互換性はないですが、当該論文にて提案されている改善策を取り込むのも一案かもしれませんね。
次の記事
読者になる
一緒に新しい世界を探求していきましょう。


















ディスカッション